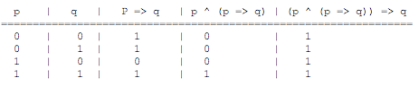
(P ^ (P => Q)) => Q named Modus ponens meaning affirms by affirming – affirming the antecedent/premise P
If the compound statement (P ^ (P => Q)) => Q is given and is true (it is always true) and P => Q is true then P must be true – therefore Q must be true (see truth table to follow the reasoning).
P => Q (If P => Q is true then...)
P (must be true)
therefore Q must be true.
In English:
P = today is Tuesday
Q = I will go to work
If today is Tuesday, then I will go to work.
Today is Tuesday.
Therefore, I will go to work.

In instances of modus ponens we assume as premises that p => q is true and p is true. Only one line of the truth table – the last – satisfies these two conditions. On this line, q is also true. Therefore, whenever p => q is true and p is true, q must also be true
3 no namers – logical implications
Hypothetical Syllogism – a logical implication
Disjunctive Syllogism – a logical implication
Simplification – a logical implication
Addition – a logical implication
Modus tollens – a logical implication
Modus ponens – a logical implication
Logical Implications
see Wikipedia